QUESTION IMAGE
Question
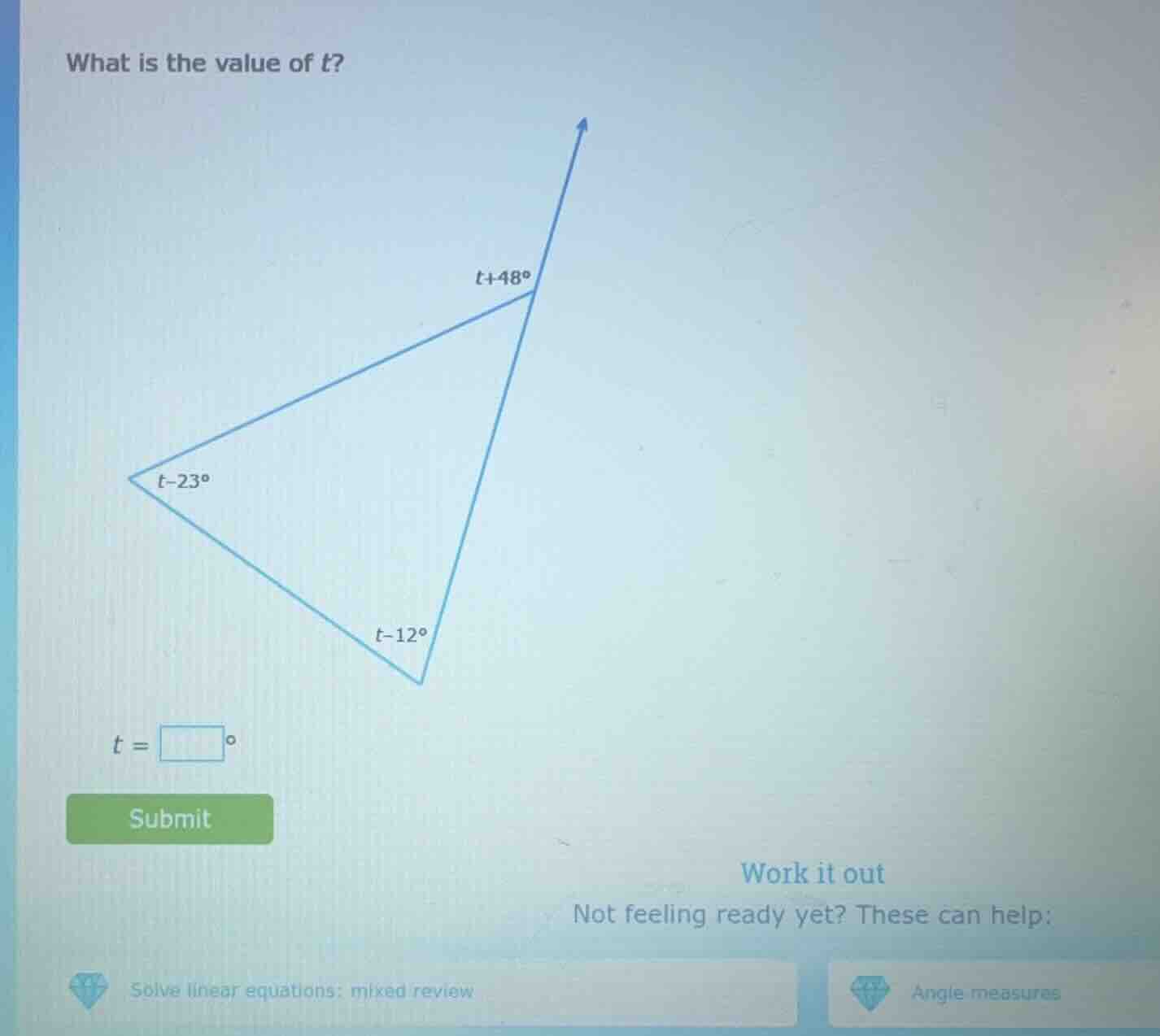
what is the value of t?
$t-23^\circ$
$t-12^\circ$
$t+48^\circ$
$t = \square^\circ$
submit
work it out
not feeling ready yet? these can help:
solve linear equations: mixed review
angle measures
Step1: Use exterior angle property
The exterior angle of a triangle equals the sum of the two non-adjacent interior angles. So:
$t+48^\circ=(t-23^\circ)+(t-12^\circ)$
Step2: Simplify right-hand side
Combine like terms on the right:
$t+48^\circ=2t-35^\circ$
Step3: Isolate variable $t$
Subtract $t$ and add $35^\circ$ to both sides:
$48^\circ+35^\circ=2t-t$
$83^\circ=t$
Explanation
Step1: Use exterior angle property
The exterior angle of a triangle equals the sum of the two non-adjacent interior angles. So:
$t+48^\circ=(t-23^\circ)+(t-12^\circ)$
Step2: Simplify right-hand side
Combine like terms on the right:
$t+48^\circ=2t-35^\circ$
Step3: Isolate variable $t$
Subtract $t$ and add $35^\circ$ to both sides:
$48^\circ+35^\circ=2t-t$
$83^\circ=t$
Answer
$t=83^\circ$