QUESTION IMAGE
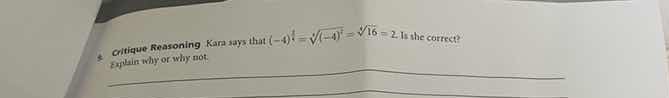
Question
- critique reasoning kara says that $(-4)^{\frac{1}{2}} = sqrt{(-4)^1} = sqrt{16} = 2$. is she correct? explain why or why not.
Step1: Evaluate left-hand side
$(-4)^{\frac{1}{2}}$ represents the square root of $-4$. In real numbers, $\sqrt{-4}$ is not a real number (it is the imaginary number $2i$).
Step2: Evaluate middle expression
$\sqrt{(-4)^2} = \sqrt{16}$. The square root of a non-negative number gives the non-negative root, so $\sqrt{16}=4$.
Step3: Evaluate right-hand side
$\sqrt{16}=4$, not 2. Also, the initial step of equating $(-4)^{\frac{1}{2}}$ to $\sqrt{(-4)^2}$ is invalid because $a^{\frac{1}{2}}$ is defined as $\sqrt{a}$ only when $a\geq0$ for real numbers.
Kara is not correct.
- $(-4)^{\frac{1}{2}}$ is not a real number (it is imaginary, $2i$), so it cannot equal a real number like 2.
- $\sqrt{(-4)^2}=\sqrt{16}=4$, not 2.
- The rule $a^{\frac{1}{2}}=\sqrt{a^2}$ does not hold for negative $a$ in the real number system, as square roots of negative numbers are not real, and $\sqrt{a^2}=|a|$ for real $a$.